Multiview - a new approach for PBFT implementation
Problem
Many well-known approaches to implementing the Proof of Stake consensus such as Tendermint [1], Hotstuff [2] and PBFT [3] are bi-modal: the protocol typically consists of a simple normal path where a leader makes proposals and everyone votes. When the normal path fails, the protocol switches to a much more complicated fall-back mode typically called a “view change”. In the view change phase, participants use the same communication process to reach an agreement on the new view before they can go back to the normal path of producing blocks.
Incognito’s BFT proposes a simpler approach. Instead of reaching an agreement on a single view, participants could see multiple views; the communication process for the view change in existing approaches is now used to propose the new block. Participants may have multiple different views, but when the majority (> ⅔ participants) commits a new block, this means that they have the same agreement on this view. If they continuously produce blocks on this view, i.e. this view dominant and achieves finality.
Preliminaries
The number of malicious nodes in the network cannot simultaneously equal or exceed ⅓ of the overall nodes in the system in a given window of vulnerability.
Requirements for the nodes are that they are deterministic and start in the same state. The final result is that all honest nodes come to an agreement on the correct and longest chain.
Multiview PBFT details
Phases in Incognito’s Multiview PBFT

PROPOSE PHASE
- Block Proposer broadcasts PROPOSE_MESSAGE and proposed block to Validators.
VOTE PHASE
Validator broadcasts VOTE_MESSAGE and collects valid VOTE_MESSAGE(s).
- After bounded time T, if |VOTE_MESSAGE(s)| > ⅔ COMMITTEE_SIZE then continue to the commit phase.
- Otherwise, wait for the new propose phase.
COMMIT PHASE
- Validator combines VALIDATOR_SIGNATURE(s) and includes it in the block and COMMITS it to the chain. Then move to the new propose phase.
In a normal case, Incognito’s PBFT is quite similar to other PBFT protocols. A node is selected as a proposer which will propose a block; other committee members vote for the block to be appended to the chain. Proposers are selected in round-robin fashion based on their id in the committee.
If a normal case fails, due to:
- A byzantine proposer not proposing a new block, or proposing multiple blocks in a single round.
- Not collecting enough votes because vote messages are delayed.
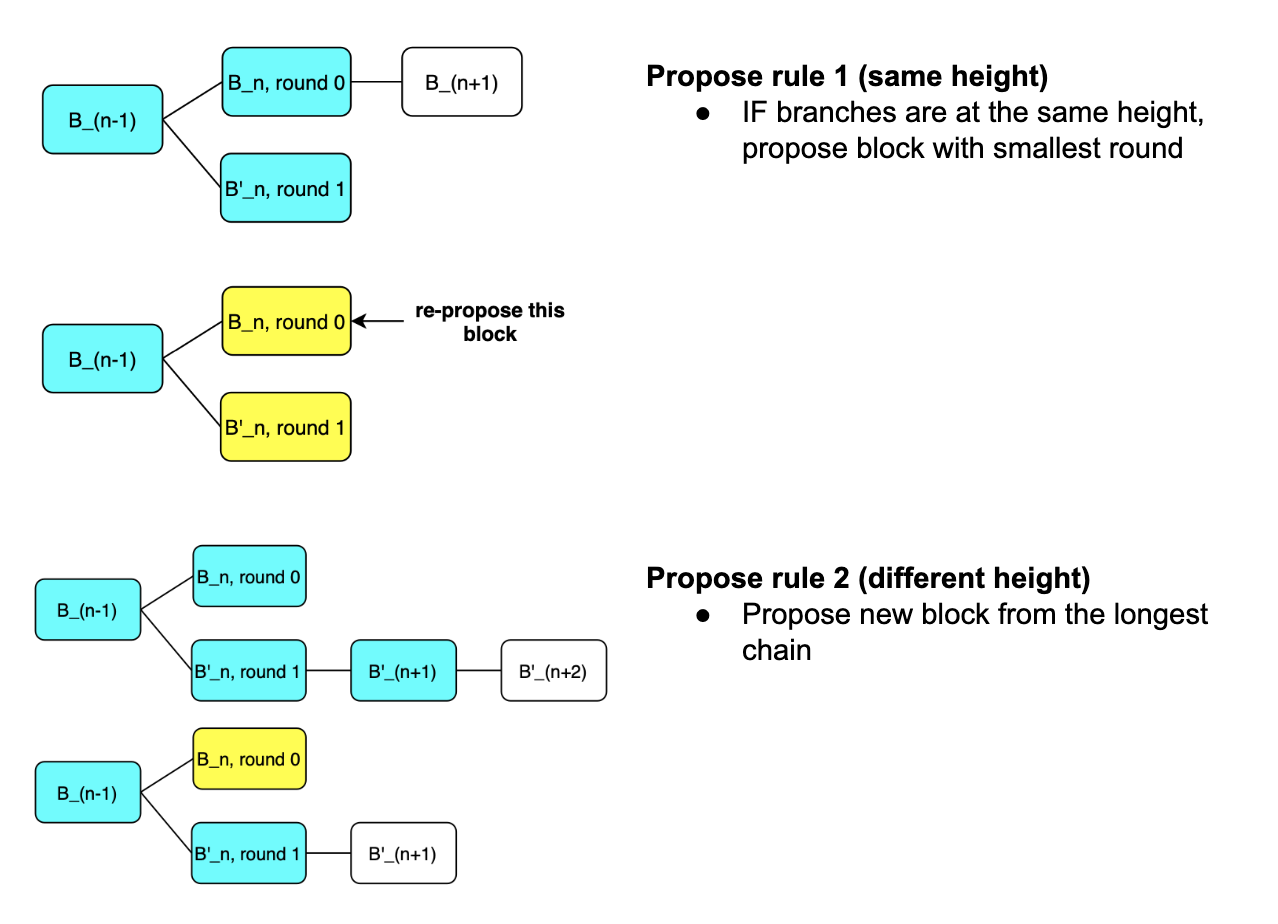
Committee members would then see many different views. In order to restore the common view of all nodes, two general rules are applied:
- Do not try to propose many different blocks at the same height
- Follow the majority group
Vote rules & Propose rules
To achieve consensus without agreement on view change, nodes in Incognito’s committee have to use the following Vote rules and Propose rules
Let

Two vote rules for:
- Branches with the same height
- Branches with different heights


Two Propose rules for:
- Branches with the same height
- Branches with different height
Lemma 1. (Finality 1) If two consecutive blocks B(n) & B(n+1) on the same branch are committed in two consecutive time slots, then block B_(n) is finality.

Proof. When block n is committed at time slot t, and block (n+1) is proposed at time slot (t+1), this implies that block (n+1) is proposed for the first time. This also implies that > 2/3 members received, agreed and voted for it. This means any further proposed block with height (n+1) will not get enough votes to commit, following Vote Rule 1. And following Vote Rule 2, no branch can grow any longer than the one with block n.
Lemma 2. (Finality 2) If two consecutive blocks B(n) & B(n+1) on the same branch are committed in time slots t and (t+i), respectively, where B(n+1) is first proposed at time slot (t+1), and this block is reproposed at every time slot t+2, t+3, ..., t+i then block B(n) is finality.

Proof. Since the block n is committed at t, and block (n+1) is committed at (t+i) with time slot (t+1), meaning that block (n+1) is first proposed at (t+1). This implies that block (n+1) with time slot (t+1) is the latest one, and > 2/3 members received, agreed and voted for it. This means any further proposed block (n+1) won't get enough votes to commit by Vote Rule 1. Moreover, during the time slot t+1, t+2,.. , t+i, no other blocks rather than the block (n+1) with time slot (t+1) are proposed or committed. Due to Vote Rule 2, no branch can grow any longer than this one.
Finality Theorem IF a block at height h is first proposed and committed in the same time slot, THEN it is finalized.
IF a block at height h is first proposed in the time slot t, it is committed in the time slot t+n, for n > 1, and it is re-proposed in the consecutive time slots: t+1, t+2,…, t+n, THEN it is finalized.
Proof.
By proposing rules 1 and 2, the proposed block at height h is always in the longest chain (i).
Following vote rule 1, any order block at height h cannot be committed because it cannot collect enough votes. In order words, the chain cannot create multiple branches at height h (ii).
Therefore, to be committed, any new proposed block must append to this block. No branch can grow any longer than this one. (iii).
(i), (ii), & (iii) imply Finality Theorem.
 *Fig 3.* Example finality cases by the finality theorem.
*Fig 3.* Example finality cases by the finality theorem.Analysis
Observation 1. If block bn is finality, then further blocks are appended to the branch containing bn, any other branch b’n is made obsolete. If a new block is successfully appended to another branch, say b'n, then more than ⅔ participants don’t agree bn is finality. This is a contradiction.
Theorem 1 (Consistency proof). Let chain ch := b1b2…bnbn+1 and chain ch’ = b’1b’2…b’nb’n+1
where bn+1 and b’n+1 are finality, and if bn+1 = b’n+1 then bi = b’i for i[n].
Proof. bn+1 and b’n+1 are finality, which means that bn and b’n are finality, if bn ≠ b’n, which either violates Observation 1 or the assumption that ⅔ participants are honest. 𑃰
Theorem 2 (Liveness proof). If some honest participant receives some transactions, this transaction will eventually be included in all honest participants’ finalized chains.
Proof.
Observation 2. Proposer is selected in round-robin fashion. Any participant will eventually be a proposer. It can then include the transaction in proposed blocks.
Observation 3. If two blocks at the same height are committed, then the block proposed earlier must be committed later. Following Propose rule 1, nodes voted for the block with a smaller round only. If ⅔ nodes voted for the first proposed block, they won’t vote for the later one.
Consider the worst case scenario where two chains are growing to infinity. In order for this to happen, the following conditions must be satisfied:
- ⅔+1 weak participants don’t collect enough votes to commit any block, however they can vote for both chains as in Fig 1. The other ⅓ power participants could commit and propose new blocks.
- Proposers in group ⅓ power participants are divided into two groups, and are alternately selected to propose blocks on chain 1 and chain 2.
- When a participant proposes a block, the next proposer will not receive any message in this round, so it can propose a block on the other chain.
Let N be the number of participants. When network traffic is peaking, assume that the probability of successfully transmitting a message between two participants is 0.5. The probability of a participant not receiving any messages in a single round is then (0.5^N)^2. This probability is negligible when N is large. Moreover, the probability of a participant not receiving any messages in x rounds is (0.5^N)^(2x). This is exponentially decreased when the number of rounds is increasing. These conditions above are thus impossible to hold through many rounds. In order words, the liveness property is guaranteed.

Fig 1. Fork case
Multiview PBFT vs Tendermint[1]
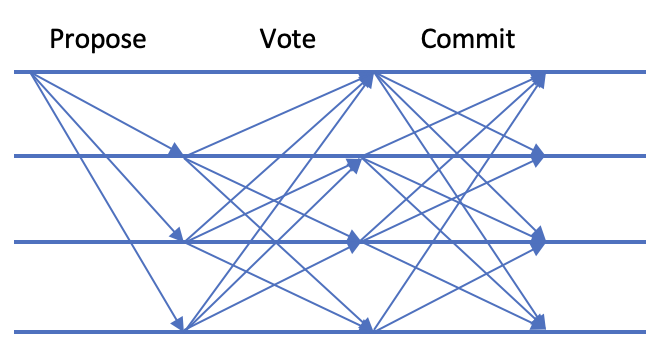
Fig 5. Tendermint operation in normal cases
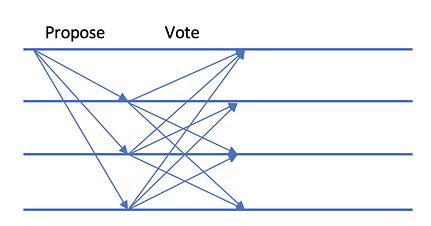
Fig 6. Multiview PBFT operation in normal cases
| Tendermint | Multiview | |
|---|---|---|
| Total messages | n + 2n^2 | n + n^2 |
| Number of phases to commit | 3 | 2 |
| Throughput (T being the delay in transferring a message) | 1/(3T) | 1/(2T) |
Conclusion
The multiview PBFT approach is simple but has many advantages:
In normal cases, Multiview PBFT increases throughput by 33% over Tendermint, and the total number of exchange messages decreases nearly 50%. Both Tendermint and Multiview PBFT can achieve instant finality in one block.
Network peaking: In the Tendermint approach, if more than ⅓ of validator vote messages arrive late, participants will repeatedly communicate to change to the new view and no block can be committed. In a Multiview approach, a block can be committed and appended to the chain.
The approach of Multiview PBFT has a natural philosophy. The consensus respects the majority group; the powerful node – which can commit blocks during bursts of network traffic – can advance the chain to new height during heavy network traffic.
Reference
[1] https://tendermint.com/static/docs/tendermint.pdf